作者： xsg

生活的真相就是，你担心的事情，99% 都不会发生；已经发生的事情，99%都没有你想象的那么严重；以前觉得很严重的事情，99% 都在你能够承受的范围之内。 —卡耐基

今年发生了三件事，影响着我对未来的思考，影响着刘霞和我之后的人事构架：4月底5楼夜谈，迫不及待，连五一假期都等不及。(too young too simple,so naive，我极为惋惜的是，也不年轻了！居然毫无职场经验)、知音楼事件(暴露出的懈怠)、全员会议（僭越）。

永远记住，别人的错误，不是你的机会！像高翠翠一样，把你自己的事干好，多一句话也别说，我问你你再说。我不问，you’d better shut your mouth up! 除了老张，你们的智力都不如我，所以，你们基本没告诉我该怎么干的能力。It’ me who tell you what to do and you just do it.

7月临阵换将，弄的我措手不及，只好亲临一线，还好，小有所成。Nobody else except me!

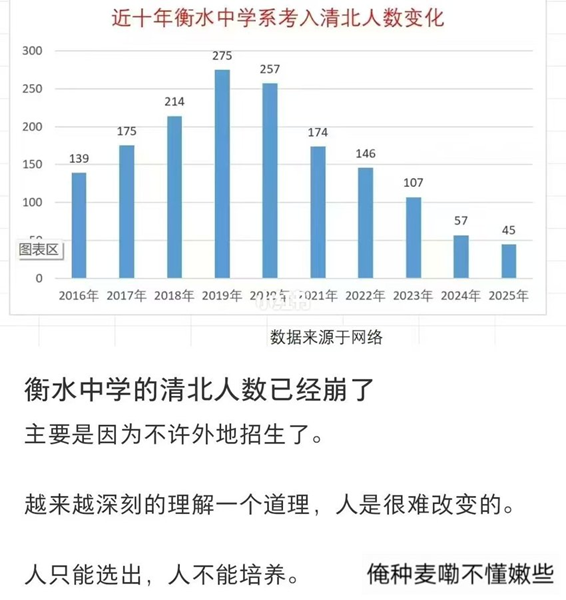
建大，西工大毕业的离职，今年又走了4个非常优秀的待富青年。学生少更留不住人。知音楼事件后，我下决心不顾一切顺序，随心所欲。

十年磨一剑。我不知道我还能不能再铸造一把。若成，还能为新曙光再续十年的命。若否，则新曙光难逃被强大的资本拍死的厄运。

不但新曙光如此，所有中等机构都是如此。老板心灰意冷，无心恋战，树倒猢狲散，最终，还想留在这个行业的，成为独立老师。

成败就看下一剑能否打磨成功。

这些二十几岁的待富青年，他们赤贫，他们有干劲。选材的标准：Loyalty,loyalty is above all else.

平庸的人有一条命，性命；
优秀的人有两条命，性命和生命；
卓越的人则有三条命，性命、生命和使命。它们分别代表着生存、生活和责任。

It’s my duty for your well-being.

凡是倒闭的公司，70％都在墙上挂过“厚德载物”，如果再出现“天道酬勤”，倒闭几率增加20%，若以上两种和“宁静致远”同时出现，基本没救了。

只要还活着的就会被羡慕。保持在场！

Erdös published more than 1,500 papers and did mathematics 19 hours a day, even at 83 – “The 1st sign of senility is when a man forgets his theorems. The 2ns sign is when he forgets to zip up. The 3rd sign is when he forgets to zip down”

互联网圈大佬，活的明白的只有丁磊和张朝阳。一个整天没愁事，一个天天忙着健身，研究数学。

以前总有人嘲笑搜狐掉队，现在才回过味儿来，人家早就活在终点线了。
在这个全员焦虑的时代，有一种最高级的炫富，叫“我不陪你们玩了”。

另外一个我完整听2个小时的，是张泽天的第一次课。

说说讲课，说说数学，这是2个层面的东西。

卓卓来了4年，已经是个很成熟的老师了。从课堂语言，跟学生的交互，我都很满意。没有了初登讲台的拘谨，非常从容，谈笑自如。这是讲课的层面。

有一个体制呢的校长跟我谈过，说培养一个成熟的老师，需要3年的时间。

这是什么意思呢？3到4年，你就会讲课了，外行看，不会认为你是生瓜蛋子。数学老师，有2个层面的东西：讲课和数学。讲课基本就到顶了，但数学，永无止境。

这就是我为什么要求，新曙光的数学老师，必须永远做高考题。你的专业知识越深厚，你能教的学生就越多。你能教小学，能教初中，能教高中。这里面更深的要求，不是讲课的技能，是数学的深浅。

举一个例子。就是今天卓卓上课的例子。说说普通老师跟我的差距。

孩子在做初一的一个程序流程图的题，随口说了一句，步长，死循环。卓卓听不出来这有什么特别的，我就能。我立刻就问学生，你上哪看的这两个词。孩子妈妈说，前面学过Python。

其实我今天不是来听卓卓上课的，我是来评估这个学生的。

新曙光培养过陕西省信息学竞赛省队的选手。目前还有学生在大厂从事大模型的研发。

总之，我对新曙光老师的要求，我不太在意你会不会讲课，我特别在意你的数学水平。因为，只要给足实践机会，经过几年的磨练，所有人都会讲课，但数学是有瓶颈的，我要求你们，把做高考题当成日常项目，你让学生练，你自己也得练。

其实，我只去过卓卓教室一次，还不是去听课，是去拍照的。

徒儿们，给我做题。我不担心你们的舌头，我担心你们的脑子。就有刚毕业的大学生，着不住新曙光数学培训的难度，不来了。

当你直接用自然语言告诉 AI “我要什么效果”，然后代码瞬间生成

转：我就是程序员出身，几乎把程序员所有的岗位，全部都齐刷刷干了一遍。
最近也在用 AI 编程开发网站，我一边享受着 AI Coding 的极致爽感，一边感到彻骨的悲凉。
我们99%的程序员，真的很难再比 AI 开发出来的东西好了！
不得不承认一个残酷的事实： 2025年11月，就是人类编程历史的“分界线”。

新曙光微信：

2026届高校毕业生规模预计1270万人，同比增加48万人。

如果还没找到工作，来新曙光试试吧。微信：

高赞回复:
其他超级大国基本上一崩溃就消失了，大家各过各的，比如罗马、波斯、奥斯曼，只有中国每次一崩溃，各路军阀跟疯了一样非要统一全国，明明当割据势力也可以吃香喝辣，不行，天无二日，民无二主，每一个大佬都有一个统一全国的梦想，历史上超级大国很多，但几千年还存活至今的超级大国只有一个。

新曙光微信：